Electrons in solids cause various physical phenomena such as superconductivity and other remarkable phase changes. Furthermore, it has become clear that in materials with strong electron-electron interaction (strongly correlated electron systems), superconducting states and metal-insulator transitions, which are qualitatively different from the conventional ones, will occur, and research is entering a new phase.
In our laboratory, we mainly synthesize oxides and carry out material synthesis and single crystal growth, and weigh thermodynamic quantities such as specific heat and electrical and magnetic properties at extremely low temperatures up to 10 millikelvin and at temperatures up to 18 Tesla. By clarifying under a magnetic field, we are proceeding with research from the perspective of responding to this new situation.
Some items are overwriting. We plan to enhance the content in the future.
Introduction to solid-state quantum physics (for undergraduate students)
First, I will briefly explain the superconductivity and magnetism that are the subjects of our research.
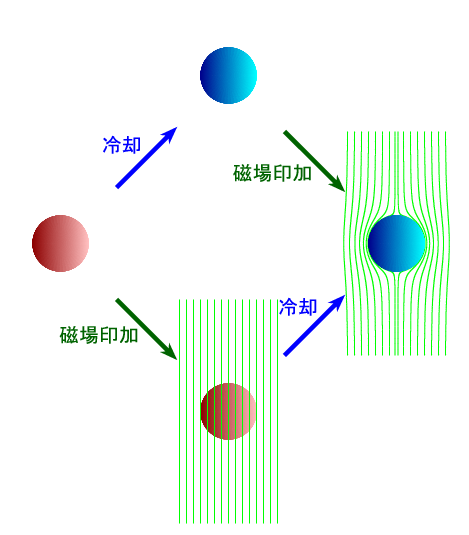
Superconductivity is a phase transition phenomenon in which “electrical resistance is zero” and “the magnetic flux density inside a substance is zero (Meissner effect)”. Since the discovery by Kamarin Onnes in 1911 that mercury becomes superconducting below 4.2 K, many substances have been discovered to become superconducting.
Substances that become superconducting
Many people think that superconductivity is a rare phenomenon, but in fact, hundreds or more kinds of substances become superconducting. However, the superconducting transition temperature ( T c ) is low. Aluminum ( T c = 1.1 K) and lead ( T c = 7.2 K) are also superconductors. As a simple element, most substances other than magnetic substances and precious metals (copper, silver, etc.) become superconducting.
Highest T c history
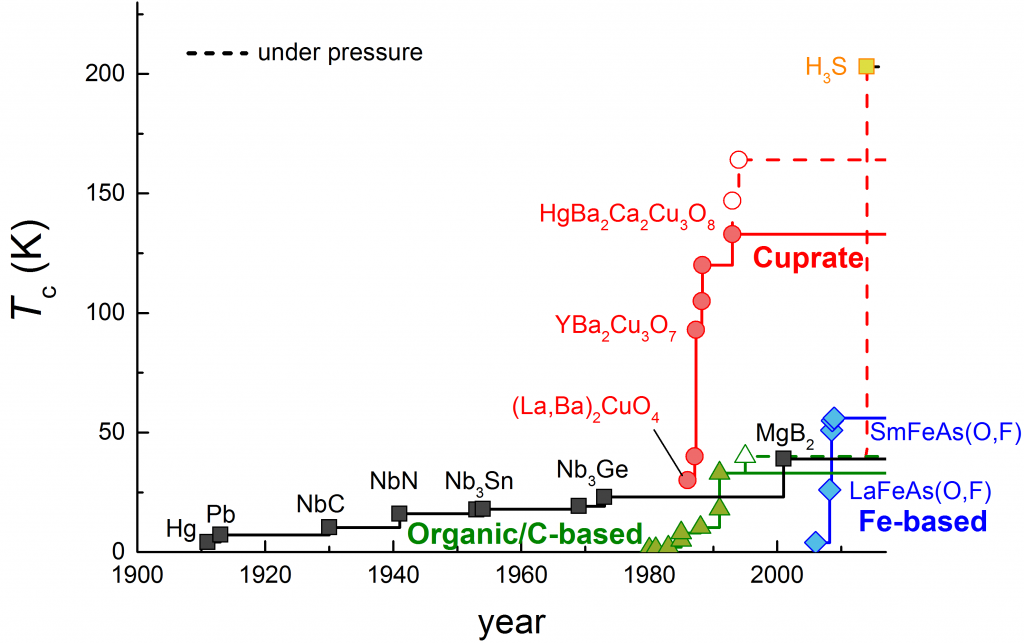
Since the discovery of mercury superconductivity, many people have been searching for substances with high T c . However, at the beginning, the transition temperature rise was slow. In 1986, Bednorz and Müller reported that doping a carrier, which was previously an insulator, with a carrier would result in superconductivity. Its superconducting transition temperature (30 K) is higher than any of the superconductors discovered at that time. A few months later, YBa 2 Cu 3 O 7- x, which exhibits superconductivity above 90 K, was discovered. The fever of high-temperature superconductivity search happened. Currently, the best under atmospheric pressure T c materials exhibiting the HgBa 2 Ca 2 Cu 3 O x is 133 K of. Furthermore, in August 2015, it was reported that hydrogen sulfide causes superconductivity of 203 K under ultrahigh pressure (~ 150 GPa). Realization of room temperature superconductivity is becoming more realistic.
Theory of superconductivity
Superconductivity is understood to occur when two conduction electrons form a “Cooper pair”. Coulomb repulsive force usually works between the electrons, but an attractive force is generated between the electrons due to the electron-lattice interaction. This theory was advocated by Bardeen, Cooper, and Schrieffer in 1957, more than 40 years after the report of mercury superconductivity, and is called the BCS theory after the proponents. BCS theory can explain many experimental results. However, in recent years, “unconventional superconductivity” that cannot be explained by this theory has been discovered, and a more comprehensive theory is needed.
Magnetism is a property that appears when (electrons) spins are periodically aligned. They are classified according to the type and arrangement of electrons that are the origin, and have various effects on various physical quantities.
Types of magnetism
The magnetism exhibited by electrons localized at atomic sites is called “localized magnetism”, and the magnetism exhibited by conduction electrons is called “itinerant magnetism”. Also, the spins are classified as follows.
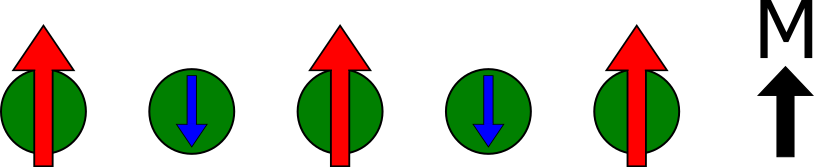
Ferromagnetism
Ferromagnetism is when spins are aligned in the same direction. It has a large bulk magnetization and hysteresis in the magnetization curve.

Antiferromagnetism
Anti-ferromagnetism means that spins are aligned antiparallel to each other. Bulk magnetization is almost zero (not a large negative value). Note that it is confused with the diamagnetic property of superconductivity.

Ferrimagnetism
Ferrimagnetism is when spins of different sizes are antiparallel to each other. The difference between them is the bulk magnetization.
Weak ferromagnetism (canted antiferromagnetism)
Antiferromagnetism that is slightly deviated from antiparallel is called weak ferromagnetism or tilted antiferromagnetism. The shifted amount appears as bulk magnetization.

Incommensulate antiferromagnetism
Antiferromagnets that have periodicity that is offset from the lattice spacing are called non-matching antiferromagnets. The ones with the same lattice spacing are sometimes referred to as matching antiferromagnetism. It is close, but it has helical magnetism, etc., but strictly speaking (I think).
Interesting phenomena about magnetism
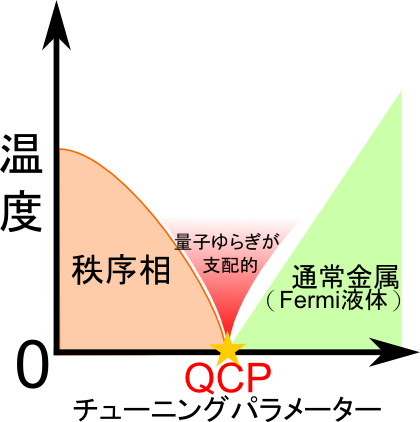
One of the interesting phenomena related to magnetism is the quantum critical phenomenon. The magnetic transition temperature can be changed by changing tuning parameters such as pressure, magnetic field and chemical displacement. The point at which the magnetic transition temperature is continuously suppressed by using these parameters and the temperature reaches absolute zero is called the quantum critical point. In the vicinity of the quantum critical point, unlike ordinary phase transitions dominated by thermal fluctuations, quantum fluctuations due to antagonism of quantum mechanical interactions are important, and non-trivial temperature dependence reflecting system characteristics in various physical quantities, Parameter dependence appears. Also, a superconducting phase may appear near the quantum critical point. This superconductivity is likely to be an unconventional superconductivity in which quantum fluctuation is important for the attractive force between electrons, and is one of the important research themes.
Next, I will explain the research methods used in our laboratory.
Crystal growth is the starting point for solid physics research. We are searching for new materials such as superconductors that exhibit novel phenomena. So far, for example, silver lead oxide superconducting Ag 5 Pb 2 O 6 , quasi-two-dimensional conductor PdCoO 2 showing giant magnetoresistance , space-reversal symmetry breaking superconductor CaIrSi 3 , new superconductor La 3 Pt. 4 , and we have been synthesizing the first superconductor such as Sr 3- x SnO in the reverse perovskite oxide and purifying the crystal.
The basis of crystal growth is to mix the raw materials and bake. Since the conditions under which a substance stabilizes are various, various types of furnaces are used to search for optimum conditions. Recently, there are many opportunities to synthesize anaerobic substances (which oxidize and decompose when exposed to air), and sometimes a glove box in which Ar gas is circulated is used. Below, we introduce the two crystal growth methods that our laboratory mainly uses.
Flux method
Flux is a substance added to lower the melting point of a substance. A single crystal can be obtained by putting a mixture of the target substance and flux in a crucible, raising it to a liquid temperature, and then slowly cooling (hopefully). Since the quality and size of the single crystal obtained varies depending on the type and proportion of flux, trial and error is required to obtain a large, pure crystal. By the way, when the flux is the same as the element in the target substance (eg Sn flux for Sr 3- x SnO), it is called the self-flux method.
Floating zone method
Floating zone (FZ) method is a method of obtaining a single crystal by heating and melting a rod-shaped polycrystalline sample, connecting it with the lower single crystal that becomes the seed crystal, and moving the whole downward, cooling the melt part. is. Since no crucible is used, it is easy to obtain a pure single crystal. You can also get a large sample.
The prepared crystal sample is evaluated using an X-ray diffractometer, Laue and EDX.
In order to discover novel superconductors and magnetic materials, we are synthesizing new substances and performing pure single crystal crystallization.
Bulk measurements such as electrical resistance measurements are used to investigate the basic properties of materials. By using MPMS and PPMS, the electrical resistance of 1.5 K or more, magnetization, and specific heat can be measured relatively easily. Furthermore, the measurement range can be expanded to around 0.1 K by using a dilution refrigerator, 3 He refrigerator, and adiabatic demagnetization refrigerator.
Electrical resistance measurement and magnetization measurement are important measurement methods for understanding the basic properties of substances.
We will briefly introduce the principle of nuclear magnetic resonance (NMR) and its positioning in solid state physics, and also touch on the research content in our laboratory.
The principle of NMR measurements
Some nuclei have a nuclear spin and a magnetic moment. Their magnitude is as small as 10 -3 to 10 -4 times the magnetic moment of electrons , and they do not become magnetically ordered in a solid unless they are made so cold. Therefore, it can be considered that there are many small “magnets” called atomic nuclei in a solid.

Nuclei with nuclear spin exhibit the Zeeman effect under an external magnetic field . That is, the nuclear spin level splits, the nuclear magnetic moment is polarized, and the “magnet” is aligned in the direction of the magnetic field. When an oscillating magnetic field (high frequency) with an energy equal to the level interval is applied to it, the level transition occurs. This is called nuclear magnetic resonance . When resonance occurs, the nuclear spin falls in a direction other than the magnetic field direction. This resonance can be detected as an induced electromotive force due to absorption of a given high frequency or rotation of the collapsed nuclear magnetic moment around the static magnetic field (Larmor precession).
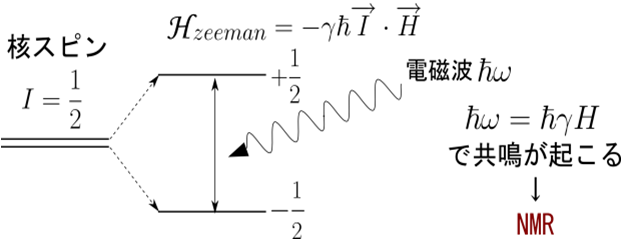
In reality, due to the small nuclear magnetic moment, the degree of alignment of the “magnets” of the nuclei in the magnetic field is small. Here, let’s take hydrogen nucleus 1 H, which is one of the nuclides with a large nuclear magnetic moment, as an example. 1 H has a nuclear spin quantum number of I = 1/2 and its gyromagnetic ratio γ is about 42.6 MHz / T, that is , its resonance frequency is 42.6 MHz under a magnetic field of 1 T. This spin polarization is on the order of hν / k B T (here, ν = γ H ) in thermal equilibrium, so if 1 H is placed in an environment with temperature T = 1 K and magnetic field μ 0 H = 1 T, its polarization will be It is about 10 -3 . Therefore, the nuclear spin system is in the high temperature limit under normal environment (and even at low temperature such as 100 mK).
NMR in solid state physics
Characteristic
Needless to say, the main electronic properties of solids are electrons, but NMR, which obtains signals from nuclei, plays an important role in understanding electronic properties. To list the features,
- Microscopic measurement means using atomic nuclei as a probe
- Information can be obtained separately for each nuclear site
- The target substance can be seen regardless of the impurity phase
- Spectroscopy using resonance with weak high-frequency magnetic field
- Measurement can be performed with almost no change in state in the measurement system (electronic system)
- Phase information can also be obtained (coherent)
- Both dynamic and static information of electronic system can be observed
Etc. From the viewpoint of experimental technology, NMR equipment is relatively small, and high-frequency technology has been established for a long time.
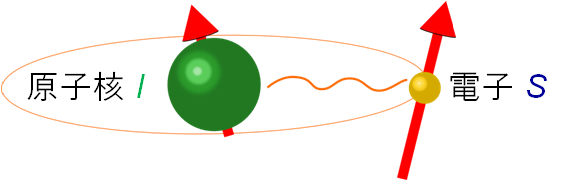
Hyperfine interaction
The reason why electronic information can be obtained from NMR in solids is the hyperfine interaction between the nucleus and the electron . The effects can be classified into static information and dynamic information. The electron spin is also polarized under a static information magnetic field, but the NMR resonance frequency deviates from γH because the polarization creates an extra magnetic field at the nuclear spin position . This shift is called the night shift and is defined as K = ( ν – γH ) / γH . The night shift corresponds to the electron spin susceptibility, but its value is much larger than the macroscopic susceptibility because the effect of hyperfine interaction is large in metals. Therefore, the NMR night shift is a powerful way to know the electron spin state, especially in the superconducting state (where the small spin susceptibility is hidden by the Meissner effect). When a high frequency is applied under a dynamic information magnetic field, the nuclear spin collapses, but eventually it returns to its original state polarized in the magnetic field direction. This is because the surrounding electron system exchanges energy with the nuclear spin system as a heat bath. This relaxation speed is called the nuclear spin-lattice relaxation rate 1 / T 1 (also known as the longitudinal relaxation rate) and reflects the magnitude of magnetic fluctuations in the electronic system. In addition, it is called nuclear spin-spin relaxation rate 1 / T 2 (both lateral relaxation rate and spin-echo decay rate), which is the speed at which the phase of Larmor precession after excitation becomes irregular (coherent collapse ). There is also a quantity.
Nuclear quadrupole resonance (NQR)
The splitting of the levels of nuclear spins is not just due to the Zeeman effect. Ions and conduction electrons produce a local electric field in a solid, but their intensity changes spatially. When the electric field gradient is combined with the electric quadrupole moment of the nucleus, the nuclear spin level is also split. This effect exists even under zero magnetic field, and the method of observing the resonance of nuclear spins without applying a magnetic field is called nuclear quadrupole resonance (NQR) . Under a magnetic field, it appears as an effect of splitting one NMR resonance line into multiples if there is no electric field gradient. NMR can be performed on nuclei with a nuclear spin quantum number of 1/2 or more, but NQR can be performed on nuclei of 1 or more.
One of the advantages of NQR is that it provides electrical information around the nucleus. The NQR resonance frequency reflects electrical properties such as the valence of the electron system and is sensitive to changes in crystal symmetry. Another advantage is that the NQR does not require an external magnetic field, so measurements can be made without disturbing the electron system in the magnetic field. For example, superconductivity is generally weakly ordered to magnetic fields, but with NQR, 1 / T 1 can be obtained without affecting superconductivity . Unlike NMR, NQR cannot control the split width of nuclear spin levels freely, and there are not as many substances that can be NQR as NMR, but if NQR is possible, information on the target substance You can bring out more.
Research theme of the NMR group in our laboratory
Lastly, I would like to list some research themes being conducted in the NMR group of our laboratory. The NMR group mainly focuses on magnetic materials and superconductors. Most of them are strongly correlated electron systems.
- Iron-based superconductor
- Uranium-based ferromagnetic superconductor
- Artificial superlattice containing heavy electron superconductors such as CeCoIn 5
- Ruthenium oxide superconductor Sr 2 RuO 4
I will briefly explain about NMR, which plays an important role in elucidating electronic properties.
The above measurement method is performed in an environment of extremely low temperature, high pressure and high magnetic field.
By using a dilution refrigerator, a 3 He refrigerator, or an adiabatic demagnetizer, it is possible to measure up to around 0.1 K (0.05 K depending on the product). Here is a simple principle.
3 He refrigerator
3 He is one of the isotopes of helium. Helium which exists naturally is almost 4 He, and the boiling point is 4.2 K under atmospheric pressure and about 1.5 K in a vacuum that can be realistically reached, but in the case of 3 He, 3.2 K under atmospheric pressure and vacuum. It drops to around 0.3 K. Therefore , immersing the sample in 3 He of liquid will cool it to 0.3 K. However, 3 He is very expensive (more than 500,000 yen for 1 liter of gas), so almost all devices are designed to contain 3 He in a closed space .
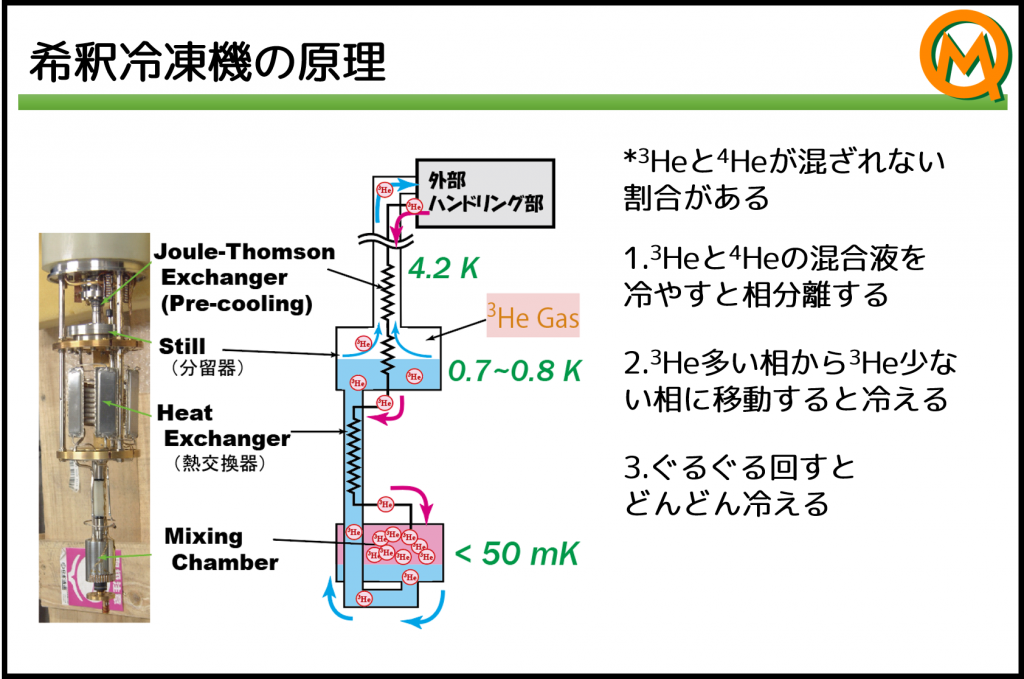
Dilution refrigerator
When 3 He and 4 He are mixed and cooled , phase separation occurs between the thick and thin phases of 3 He at low temperature . The dilution refrigerator cools by ” 3 He evaporation” that occurs between these phases . The minimum temperature that can be achieved depends on the design, but there are some that can be set to 0.01 K or less.
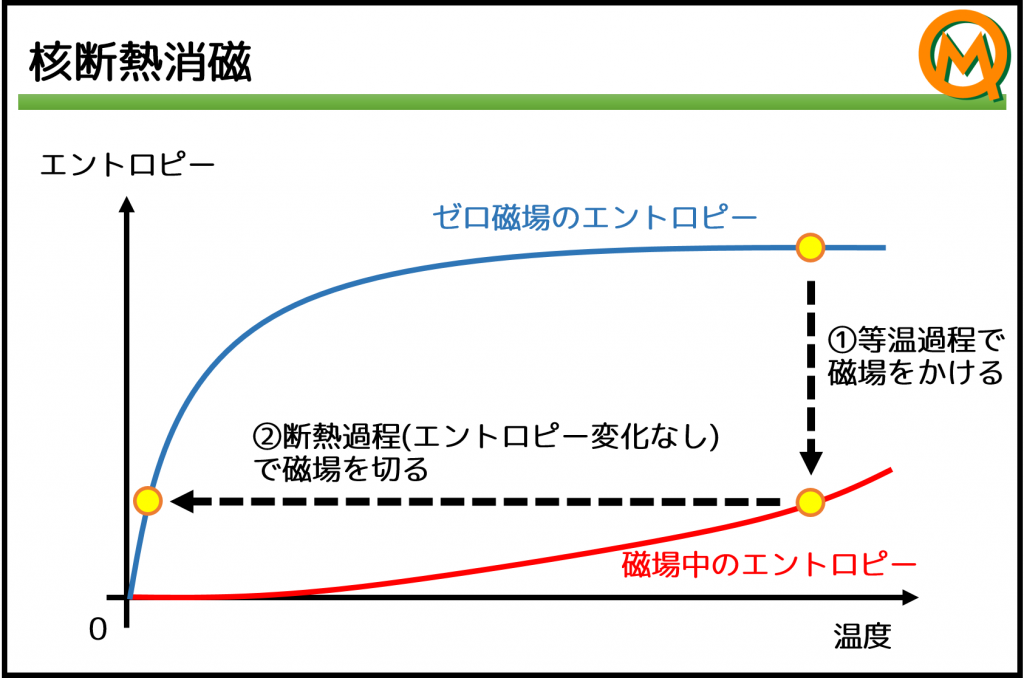
Adiabatic demagnetization refrigerator
It is a method of cooling by adiabatically reducing the magnetic field to zero while keeping the entropy small in the magnetic field. It is famous to use the nuclear spin of copper, but it is possible to cool from around 2 K to around 0.1 K by using the electron spin of a paramagnetic salt, which has a weak interaction. By combining this device with PPMS, it is possible to measure from room temperature to 0.1 K almost automatically (however, in principle, measurement at low temperature in a strong magnetic field is not possible).
down to 0.1 K (0.05 K in some cases)
Introduction
When pressure is applied to a substance, the lattice constant shrinks, and the properties of the substance such as magnetic transition temperature and superconducting transition temperature change. Pressure is one of the important parameters because it is possible to investigate the origin of superconductivity and magnetism by measuring while changing the property of a material. There are two important factors in pressure measurement: Maximum ultimate pressure of the pressure cell and sample space If a pressure cell with a high maximum ultimate pressure is used, a wide parameter space can be investigated, but the sample space becomes smaller accordingly. In measurement such as NMR measurement where the signal strength is proportional to the sample size, the sample size is also important, so it is necessary to select an appropriate one. Pressure medium In pressure measurement, hydrostatic pressure is realized by pressurizing a sample in a liquid (pressure medium). Commonly used pressure media include Fluorinert, Daphne Oil, and a mixture of methanol and ethanol. These pressure media can be handled relatively easily, but many pressure cells apply a uniaxial load, so there is a constraint that when the pressure media exceeds a certain pressure, they solidify and maintain hydrostatic pressure. There is. It has been reported that hydrostatic pressure is maintained even after solidification by using nitrogen or argon, and it is an effective pressure medium when aiming for higher pressure. However, it needs to be encapsulated at a low temperature and requires advanced technology.
How the pressure cell works
Our laboratory mainly uses “piston cylinder cells” and “indenter cells” ( photo ). Here, we will explain the internal structure of the cell and the mechanism of pressurization using the former as an example.
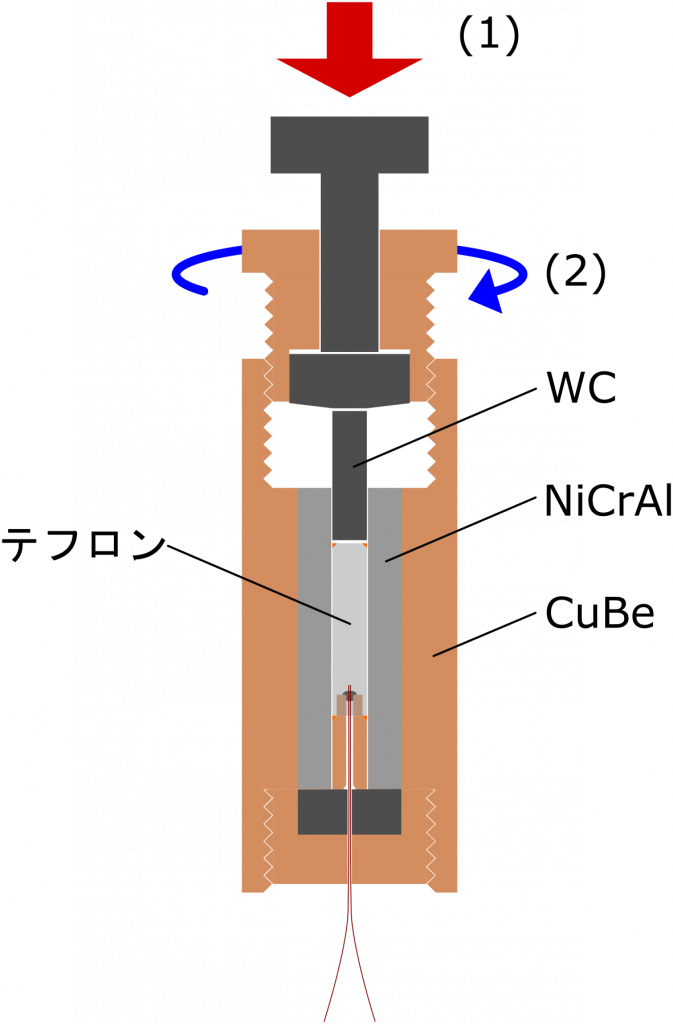
First fill the sample with pressure medium and seal. Then (1) use the internal piston to push the sample space with a large force to compress it. Hopefully, the sample will now have a pressure on the order of 1 GPa (10,000 atmospheres). Finally, (2) tighten the screw to fix the piston.
To achieve such high pressures, the cells need to be made of particularly hard material. Materials such as CuBe (copper and beryllium) alloys and NiCrAl alloys are mainly used for the body of the pressure cell in our laboratory. In addition, WC (tungsten carbide) is used for pistons that require a large force.
up to about 50 kbar
Introduction
Since the properties of superconducting and magnetic materials change when a magnetic field is applied, measurement in a magnetic field is important. Also, if it is a single crystal, I am interested in the difference in reaction depending on the magnetic field direction. A high magnetic field has a higher signal strength in NMR measurement, so a high magnetic field is desirable when measuring weak signals.
Superconducting magnet
In order to achieve a large magnetic field, a superconducting magnet (electromagnet consisting of superconducting wire) is often used. Since superconductors have the property of zero electrical resistance, they do not generate Joule heat and can carry large currents. Most of the magnets in our laboratory introduced below are also superconducting magnets. Therefore, the magnet is embedded in a cryogenic device and cooled with liquid 4 He etc. Our laboratory can apply a magnetic field of up to 16 T ( 18 T by decompressing and cooling liquid 4 He).
Some superconducting magnets have a persistent current mode. That is, since a superconductor ideally has no current decay, a magnetic field can be maintained by creating a permanent current loop without applying an external current. By doing so, the heat generated in the lead wire connecting the superconducting magnet and the power supply is eliminated, and the load on the low temperature environment is reduced.
Various types of magnets
Various types of high-field magnets are used depending on the object to be measured. Below is a brief explanation of the magnets we have. Vector magnet A vector magnet is a device that can freely control the magnitude and direction of a magnetic field, which is a three-dimensional vector field. Mainly (1) three magnets apply a magnetic field in the x , y , z directions orthogonal to each other , and (2) two magnets apply a magnetic field in the z (vertical) and horizontal directions, and the latter is rotated to There is a method to obtain dimensional freedom (see the figure below). We have one magnet for each of these methods.
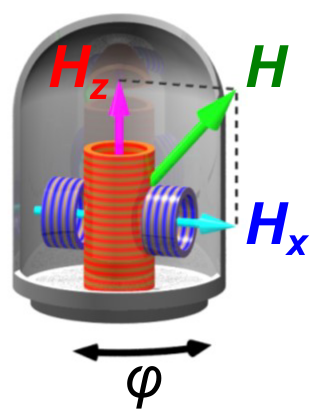
Transverse magnetic field split magnet
The transverse magnetic field split magnet is a device that has a structure in which the magnet divided into two is oriented horizontally, and can control the angle of the magnetic field by rotating the sample. Although it has less freedom of angular rotation than a vector magnet, it has the advantage of achieving relatively high magnetic field homogeneity.
High homogeneity magnet for NMR
A magnetic field with high spatial homogeneity (eg 10 -5 / cm 3 ) is required to obtain a sharp linewidth of NMR spectrum. It is also required that the time decay of the magnetic field is small. Our NMR magnets have such high homogeneity and excellent temporal stability. Some magnets are split type and can rotate at an angle.
up to 16 T (Tesla)
Finally, I will outline recent research themes.
Basic physical properties
Sr 2 RuO 4 is a superconductor with T c = 1.5 K having a layered perovskite structure, and has the same crystal structure as the copper oxide high-temperature superconductor La 2- x Ba x CuO 4 . It is characterized by a two-dimensional electronic state in which the RuO 2 surface is responsible for electrical conduction (Fig. 1).
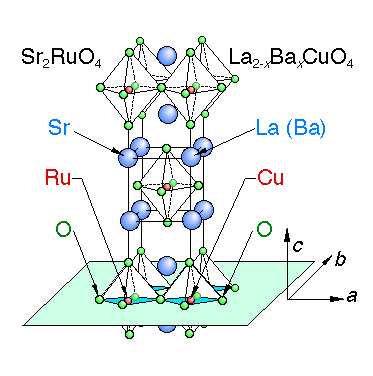
One of the reasons why Sr 2 RuO 4 superconductivity is receiving much attention is that spin triplet superconductivity may be realized. In the spin triplet superconducting state, unlike the singlet state, various interesting phenomena are expected because the Cooper pair has spin degrees of freedom. On the other hand, recently, some results that cannot be explained without spin singlet superconductivity have been reported, and their superconducting symmetry has attracted attention.
Below, I will introduce some of the research conducted on Sr 2 RuO 4 in our laboratory .
Superconducting first-order phase transition
Generally, superconductivity is destroyed by a magnetic field, and its two origins are known: the Pauli paramagnetic effect and the orbital pair destruction effect of type II superconductors. The former is because the spin susceptibility decreases in the superconducting state and the energy gain of spin magnetization becomes smaller than that in the normal state. If this mechanism is dominant, superconductivity is destroyed by the first-order phase transition at low temperatures. If the spin susceptibility does not decrease in the superconducting state, this mechanism will not work. On the other hand, the latter mechanism is always present and, if predominant, exhibits a second-order phase transition.
It was known from the early days that the superconducting state of Sr 2 RuO 4 was abnormally strongly suppressed by the magnetic field in the ab direction, but it was found from the measurement of a pure single crystal sample that the magnetic field in this direction It was revealed that the superconductivity is destroyed by the first-order phase transition at low temperature.
We would like to introduce Sr2 RuO4, which is one of the most actively researched substances in our laboratory.
Iron-based superconductors are a group of superconducting materials with FeAs or FeSe layers discovered by the Hosono group of Tokyo Institute of Technology in 2008. Due to its high transition temperature (up to 55 K) and the existence of a superconducting phase adjacent to the magnetic phase, numerous researchers are conducting research. Here, we introduce the topics of BaFe 2 (As 1- x P x ) 2 and FeSe that we are studying .
Unconventional superconductivity and antiferromagnetic quantum critical behavior in BaFe 2 (As 1- x P x ) 2
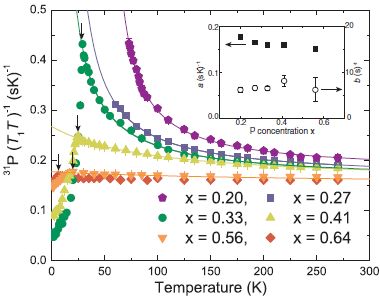
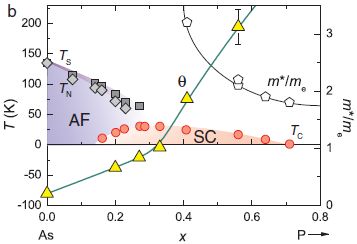
It is known that BaFe 2 As 2 which is a base material of iron-based superconductors exhibits superconductivity by various element substitutions. BaFe part was replaced with As and equivalent number of P of As Site 2 (As 1- x P x ) 2 is, T c, max ~ 31 K ( x indicates superconducting relatively high temperature and ~ 0.33) . As and P are equivalent number substitutions, so the number of carriers does not change, and it is thought that the strength of magnetic excitation can be changed without significantly changing the electronic structure. From the night shift measurement, it has been empirically revealed that P-substitution hardly changes the density of states. This point is very different from Ba (Fe 1- x Co x ) 2 As 2 with electron doping, and shows that equivalent number substitution is a good tuning parameter that can induce superconductivity without significantly changing the electronic structure. . Therefore, BaFe 2 (As 1- x P x ) 2Can be said to be an ideal stage for investigating the relationship between high temperature superconductivity and magnetic excitation. From the temperature change of the nuclear spin-lattice relaxation rate 1 / T 1 , two-dimensional antiferromagnetic fluctuations develop with increasing T c from the high P concentration region with low T c to the boundary of the antiferromagnetic phase. The behavior was obtained (Fig. 1), and it was further found that the magnetic ordering temperature θ estimated from 1 / T 1 takes a value close to 0 K in the region x = 0.33 where T c is the highest (Fig. 2). . This suggests that the antiferromagnetic fluctuation plays a central role in the development of high-temperature superconductivity in this system, and that the antiferromagnetic fluctuation originates from the quantum critical point existing near x = 0.33. I will. Superconductivity near the quantum critical point is a common behavior in heavy electron systems ( T c ~ 1 K) in which f electrons play a major role . Interestingly, a strong correlation between the quantum critical point and superconductivity was found even in iron-based superconductors where the d-electron is the main role and the energy scale is very different from the electron system. It may indicate the existence of a strong superconducting mechanism.
Pseudogap-like behavior of iron-based superconductor FeSe observed by NMR
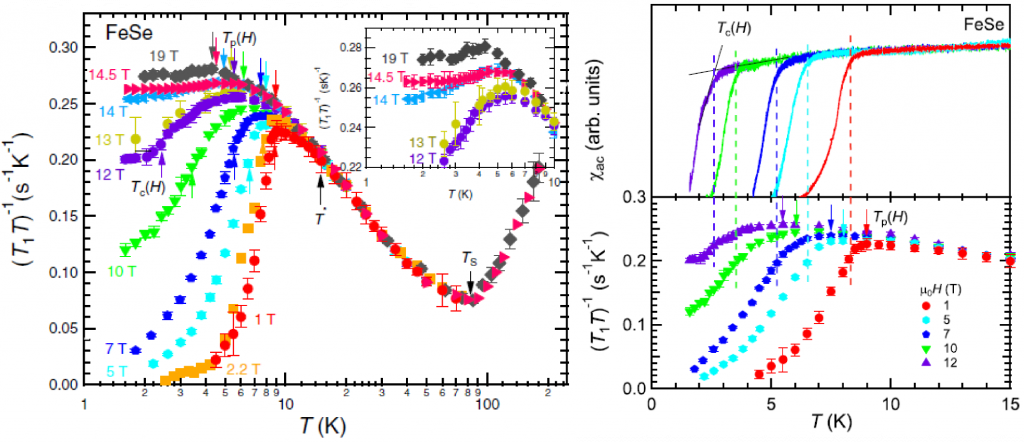
The iron-based superconductor FeSe is a peculiar iron-based superconductor that exhibits a structural phase transition at T S = 90 K, then does not show magnetic order at low temperatures and undergoes a superconducting transition at T c = 9 K. We performed nuclear magnetic resonance measurements up to a high magnetic field of 19T. The left diagram of Fig. 3 shows the temperature dependence of the nuclear spin-lattice relaxation rate 1 / T 1 T in each magnetic field . 1 / T 1 T is T S increases with the development of antiferromagnetic fluctuations in the following, T C shows a sharp decrease in the following.
In FeSe, 1 / T 1 T strongly depends on the magnetic field not only in the superconducting state but also in the normal state . T C when attention is paid to the above (Figure 3 right figure), 1 / T 1 T is T C a sufficiently high temperature than T the p- you can see that decreases from. T p decreases in the same way as T c when the magnetic field is increased. This suggests that T p is associated with superconductivity. 1 / T 1 T of T c decreases from a higher temperature than has been suggested that copper oxide high-temperature superconductor as well as strong superconducting fluctuations are present in FeSe. Pseudo-gap behavior due to such superconducting fluctuations has also been observed in other physical quantities.
I will introduce the iron-based superconductor discovered in 2008.
In normal superconductor, Cooper pair is composed of up-spin and down-spin, and the synthetic spin size S is zero. This is the spin singlet state. On the other hand, there are superconductors with S = 1 in the world, which are called spin triplet superconductors. In addition to superconductors, superfluid 3 He has realized spin triplet pairs.
The most direct way to distinguish these two types of superconductivity is to measure the spin susceptibility in the superconducting state. However, measuring the magnetic susceptibility of the superconducting state is very difficult, so other (indirect) evidence is also important. Very few substances are considered to be spin-triplet superconductivity, but UCoGe and UTe 2, which we study in our laboratory, are strong candidates.
Introducing spin triplet superconductors, which are different from ordinary spin singlet superconductors.
A brief introduction to ferromagnetic superconductors, one of the strongly correlated electron systems.
Ferromagnetism and superconductivity
In the field of solid-state physics, the theme of whether ferromagnetism and superconductivity coexist has long been discussed. Ferromagnetism is a state in which the electron spins are spontaneously aligned to produce a magnetic field, but superconductivity has the property of canceling an external magnetic field in addition to the disappearance of electrical resistance (the Meissner effect). Therefore, at first glance, ferromagnetism and superconductivity seem to be mutually opposed ordered states.
However, it was discovered in 2000 that when pressure is applied to the uranium compound UGe 2 in the ferromagnetic state, superconductivity occurs at low temperatures while maintaining ferromagnetism. Furthermore, it is discovered that URhGe and UCoGe cause superconductivity inside the ferromagnetic phase even under normal pressure. In such uranium-based ferromagnetic superconductors, it is thought that the 5f electrons of the uranium atom are responsible for ferromagnetism and superconductivity, and they coexist.
Mechanism of ferromagnetic superconductivity
In ferromagnetic superconductivity, due to its unique electronic state, it is expected that superconductivity will be expressed by a mechanism different from the conventional one. As a result of energetic research, it has become clear that these ferromagnetic superconductors are caused by ferromagnetic fluctuations . That is, in general, the electron spin directions are not perfectly aligned even in the ferromagnetic state, and fluctuate with time. In uranium-based ferromagnetic superconductors, this fluctuation is considered to be the origin of superconductivity. It has been considered that ferromagnetism and superconductivity conflict with each other, so it can be said that superconductivity of ferromagnetic origin is a major discovery.
One of the experimental evidence that the origin of the superconductivity in UCoGe is ferromagnetic fluctuations is the results of nuclear spin-lattice relaxation rate 1 / T1 performed by the NMR group of our laboratory. 1/T1 was introduced in the ” Nuclear Magnetic Resonance (NMR)” section. 1 / T1 is a quantity that reflects the strength of ferromagnetic fluctuations. This measurement was performed by applying an external magnetic field to UCoGe in the ferromagnetic state. First, 1 / T 1 takes a large value when there is no magnetic field component in the c- axis direction of the crystal. However, when the magnetic field is slightly tilted in the c- axis direction, 1 / T 1 decreases sharply. This means that the ferromagnetic fluctuation (more precisely, its c- axis component) is suppressed by the c- axis component of the magnetic field (that is, ferromagnetism is stabilized). Since the ferromagnetic moment of UCoGe has Ising anisotropy that tends to only go in the c- axis direction, it is intuitive to understand that fluctuations settle down in the magnetic field in that direction.
In fact, not only the ferromagnetic fluctuations in UCoGe, the upper critical field superconducting is a magnetic field that is disrupted H c2 also c changes sensitively to magnetic fields in the axial direction. Generally, superconductivity is destroyed when a magnetic field is applied, but in UCoGe, when a magnetic field is applied in the c- axis direction, H c2 sharply decreases, indicating that superconductivity is weak in the c- axis component of the magnetic field . On the other hand, superconductivity is insensitive to magnetic fields in other directions, and it survives fairly strongly. The suppression of strong superconductivity against a magnetic field in a specific direction cannot be explained by conventional theory, and it can be understood that the ferromagnetic fluctuation that is the origin of superconductivity is suppressed by the magnetic field in the c- axis direction. I will. The experiment to investigate the strength of superconductivity by changing the attractive interaction of superconductivity is well known as the experiment of isotope effect in the verification of BCS theory, but the 1 / T 1 experiment of UCoGe also has the same meaning. It is considered.
Superconductivity enhanced by magnetic field
As mentioned above, “superconductivity is generally destroyed when a magnetic field is applied”, but uranium-based ferromagnetic superconductors commonly have the unique property that superconductivity is enhanced by a magnetic field in a certain direction. . This phenomenon can also be qualitatively understood because the strength of the ferromagnetic fluctuation depends on the magnetic field.
There are two main known mechanisms by which magnetic fields destroy superconductivity. One is the effect of superconducting current flowing under a magnetic field to increase the energy, and the other is the Pauli paramagnetic effect described later. In any case, the stronger the magnetic field, the greater its effect, so in many superconductors, the superconducting transition temperature decreases monotonically with respect to the magnetic field. However, it is known that in a uranium-based ferromagnetic superconductor, the transition temperature shows a maximum with respect to a magnetic field in a certain direction, and superconductivity is enhanced. Especially in URhGe, a very rare phase diagram has been revealed in which superconductivity disappears once and reappears in high magnetic field when the magnetic field is increased. Moreover, it can be seen that the superconducting phase in the high magnetic field has a higher transition temperature and the superconductivity is stabilized in the magnetic field. It has been clarified that the ferromagnetic fluctuation increases in the high-field superconducting phase of URhGe, and it is considered that this fluctuation causes superconductivity.
Spin triplet superconductivity
Ferromagnetic superconductivity is expected to have other interesting properties. Most superconductors are spin singlet superconductors, but some of them have the potential for spin triplet superconductivity. One of these is these uranium-based ferromagnetic superconductors. As an experimental proof, for example, the upper critical magnetic field exceeds the Pauli limit. In a spin singlet superconductor, electrons with antiparallel spins form a Cooper pair, so there is no Zeeman energy gain under the magnetic field, unlike the normal state. In the simplest case, the Pauli limit, which is the magnetic field at which superconductivity is destroyed by this mechanism, is given by μ 0 H Pauli / T = 1.86 T c / K (that is, the Pauli limit is 1.86 T if the transition temperature is 1 K). I will. However, in uranium-based ferromagnetic superconductors, superconductivity exists even in the region far beyond the Pauli limit. It can also be said that spin triplet pairs are more advantageous than singlet pairs because superconductivity coexists with spin-oriented ferromagnetism.
The spin triplet pair is believed to exhibit various interesting properties because the Cooper pair has spin degrees of freedom. Since the candidates for spin triplet superconductivity are scarce, uranium-based ferromagnetic superconductors are expected to be an important stage for their research.
Our laboratory is still actively engaged in UCoGe research. We aim to clarify the correlation between superconductivity and ferromagnetism in more detail.
I would like to introduce the unique electronic state in which both ferromagnetism and superconductivity are realized.
A superlattice is a crystal whose periodic structure is longer than that of the basic unit cell due to the superposition of two (or more) types of crystals. In recent years, it has become possible to artificially create superlattices by improving the technology for forming thin films. In particular, the heavy electron-based artificial superlattices created by the Quantum Condensed Physics Laboratory at Kyoto University are capable of controlling strong inter-electron phases. It has been noted that it has been made possible.
In the artificial superlattice, it is very important to investigate the difference in the physical properties of each layer (crystal) and the change in the physical properties due to the difference in the state of the interface and the combination. NMR measurement plays an active role as a method that enables these measurements. I would like to introduce one topic below.
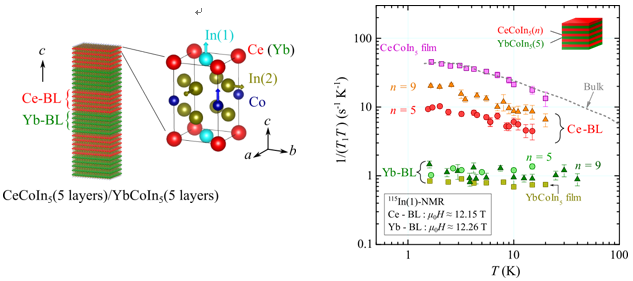
Interfacial state between heavy electron compounds and ordinary metals by nuclear magnetic resonance method with spatial resolution
Recently, an artificial superlattice CeCoIn 5 / YbCoIn 5 in which heavy electron superconductor CeCoIn 5 and ordinary metal YbCoIn 5 are alternately stacked has been fabricated (left figure), and the difference in electronic state from the bulk body has attracted interest. I will. This time, we applied the nuclear magnetic resonance method, which is a microscopic measurement method, to the CeCoIn 5 / YbCoIn 5 superlattice and succeeded in investigating the electronic states of the Yb block layer (BL) and Ce BL separately. Figure). Furthermore, by detailed spectral analysis, the signal of CeBL was divided into the interfacial layer and the inner layer, and the difference in their electronic states was clarified. It is considered that the method of this research can be applied to other superlattices, and the result of this research also means that NMR is effective in the research of superlattices.
Introducing interesting properties of artificial superlattice.
What is a topological insulator / superconductor? An insulator / superconductor whose topological number defined in some way has a nontrivial value. At the interface with the one with an obvious topological number (air or vacuum), the topological number needs to be changed discontinuously, so a peculiar interface state appears. Since this interface state is protected by the topological number, it has a strong property against impurities. Initially, the idea was for bulk insulators and full-gap superconductors, but the scope of application has expanded to include semimetals and superconductors with nodes by devising the method of defining the topological number. Is not just some topological stuff). Here is a brief description of topological.
Among the substances handled by this laboratory, Sr 2 RuO 4 , UCoGe, Sr 3- x SnO, etc. are considered to have topological properties. Introduced below is the first superconductor Sr 3- x SnO in the reverse perovskite oxide discovered by our laboratory .
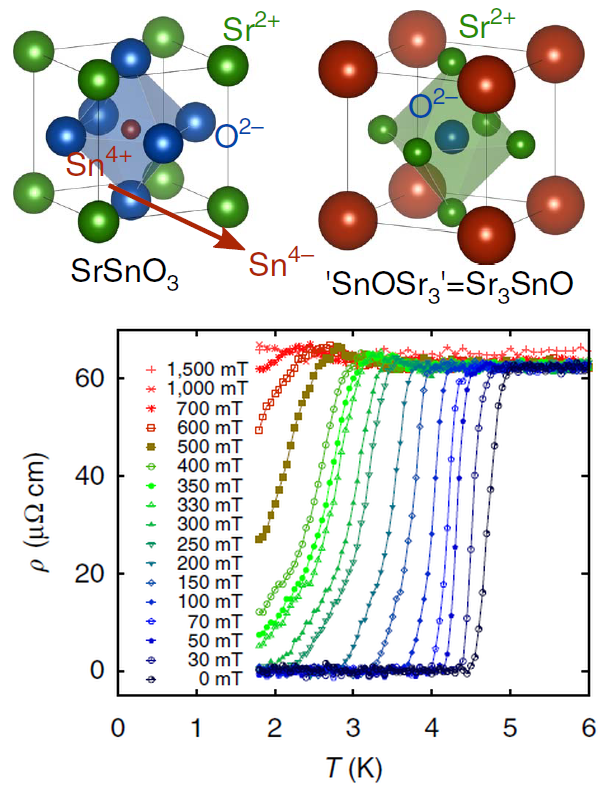
Discovery of the first superconductor Sr 3- x SnO in reverse perovskite oxide
The perovskite oxide represented by the chemical formula of AB O 3 has the simplest structure as an oxide having two kinds of metal ions, and is a very important substance in materials science and earth science. It is no exaggeration to say that he is the representative player of Oxide. In fact, perovskite oxides have a group of substances called anti-perovskite oxides, which are “siblings” that have the valences of ions reversed. It has been pointed out that this antiperovskite oxide has a property different from that of ordinary oxides, such as a negative valence of B metal ion, and may be a topological substance. We synthesized the antiperovskite oxide Sr 3- x SnO and found that this material exhibits superconductivity below about 5 K. This is the first superconductivity found in antiperovskite oxides. Also, in a joint research with the theoretical group, we pointed out that this material may be a topological superconductor. This achievement was published in Nature Communications . M. Oudah from D2, Ms. Ikeda from M2, and M2 (exchange student from Humboldt University) JN Hausmann performed experiments mainly in our laboratory. Regarding theoretical analysis, Professor Sato of Kyoto University We conducted joint research with Assistant Professor Kobayashi and others. (The figure below is taken from the relevant Nature Communications paper.)
Introducing the topical insulators and superconductors that have been the topic of recent years.
In solid-state electronic systems, the ground state often becomes some ordered state through a phase transition at low temperature due to the interaction between the constituent electrons. This phase transition temperature is often lowered to absolute zero ( T = 0) by controlling tuning parameters such as pressure, magnetic field and chemical displacement . This phase transition that occurs at absolute zero is called the quantum phase transition, and when the phase transition is quadratic (the order variable is continuous with the transition), the transition point is called the quantum critical point (QCP) (Fig. 1). .

In the vicinity of the quantum critical point, the effect of quantum fluctuation due to antagonism of quantum mechanical interaction becomes apparent, unlike the usual phase transition dominated by thermal fluctuation. Therefore, non-trivial temperature dependence and parameter dependence that reflect the characteristics of the system appear in various physical quantities. This property is called a non-Fermi liquid as opposed to the normal metallic state (Fermi liquid) . (However, in many cases, a quasiparticle picture of a Fermi liquid holds even if it is a “non-Fermi liquid”). For example, in the ordinary metallic state, the electrical resistance behaves like Δρ = ρ ( T ) − ρ 0 ~ T 2 , and the electron specific heat coefficient behaves like ΔC / T = constant, but in the vicinity of the quantum critical point, the temperature dependence differs from these. Sex is observed. The physical phenomenon caused by strong electron correlation observed near such a quantum critical point is called the quantum critical phenomenon.
One of the interesting points of the quantum critical phenomenon is superconductivity that often appears near the quantum critical point. In such superconductivity, quantum fluctuation is closely related to the attractive force between electrons required for pair formation, and the superconducting symmetry may be different from the conventional BCS theory. I am.
Below are some topics related to the quantum critical phenomenon. Both are the themes that we have been conducting research in our laboratory.
Antiferromagnetic quantum critical point of iron-based superconductors
As an example of the quantum critical point, we will introduce the antiferromagnetic quantum critical point of the iron-based superconductor BaFe 2 (As 1- x P x ) 2 . This system becomes an antiferromagnetic phase at low temperature when arsenic is 100% (BaFe 2 As 2 ), but when arsenic is replaced by phosphorus, antiferromagnetism is suppressed and superconductivity occurs. The superconducting transition temperature reaches a maximum around x = 0.33, which exceeds 30 K.
As a result of NMR performed in our laboratory, it became clear that the antiferromagnetic quantum critical point is likely to lie in the vicinity of the enhanced superconducting transition temperature. “Antiferromagnetic fluctuation” can be measured by NMR, and it tends to diverge at absolute zero at x = 0.33, so it is considered that the antiferromagnetic quantum critical point exists at this concentration. (Actually, superconductivity hides the quantum critical point). Since superconductivity is enhanced at this concentration, it can be seen that the quantum critical point of antiferromagnetism and superconductivity are closely related.

Ferromagnetic quantum critical behavior of uranium-based ferromagnetic superconductors
In the case of metallic ferromagnetism, it is known that the morphology of the quantum critical point is different from other ordered phases. In the case of the above antiferromagnetism, it is said that there is a quantum critical point in the zero magnetic field, but in the case of ferromagnetism, it appears in the finite magnetic field, and in the zero magnetic field, the ferromagnetism is not the second-order phase transition but the first-order phase transition. Expected to disappear. Therefore, it is considered that the relationship between superconductivity and quantum critical point is different from other cases. Also, since superconductivity is generally weak against magnetic fields, superconductivity does not readily appear in the vicinity of ferromagnetism.
In fact, it is known that superconductivity and ferromagnetism coexist in uranium-based compounds ( ferromagnetic superconductor ). Among them, it was reported that UCoGe has the lowest ferromagnetic transition temperature and behaves like a quantum critical point due to pressure. As a result of nuclear quadrupole resonance (NQR) performed under pressure in our laboratory, it became clear that ferromagnetic fluctuations greatly develop as the ferromagnetism disappears under pressure. This behavior strongly suggests that the ferromagnetic quantum critical point exists in the vicinity. Actually, the quantum critical point should be in the finite magnetic field, but it is thought that it is near the zero magnetic field due to the strong fluctuations. Since superconductivity also develops at the same time, it can be said that superconductivity in this system is caused by the ferromagnetic quantum critical point.
Past research
In addition to the above research, we have conducted the following research related to the quantum critical phenomenon.
- The magnetic quantum critical phenomenon in ruthenium oxide
- Heavy fermion compounds YbRh 2 Si 2 magnetic excitation near quantum critical point
Introducing quantum critical phenomena that are commonly found in solid state physics.
![]()
